
No matter your education, if you have a job, you will get the minimum wage. In this linear regression example, you can think of the constant β 0 as the minimum wage. The other two components are the constant β 0 and the error – epsilon(ε). In the USA, the number is much bigger, somewhere around 3 to 5 thousand dollars. If β 1 is 50, then for each additional year of education, your income would grow by $50. It quantifies the effect of education on income. β 1is the coefficient that stands before the independent variable.
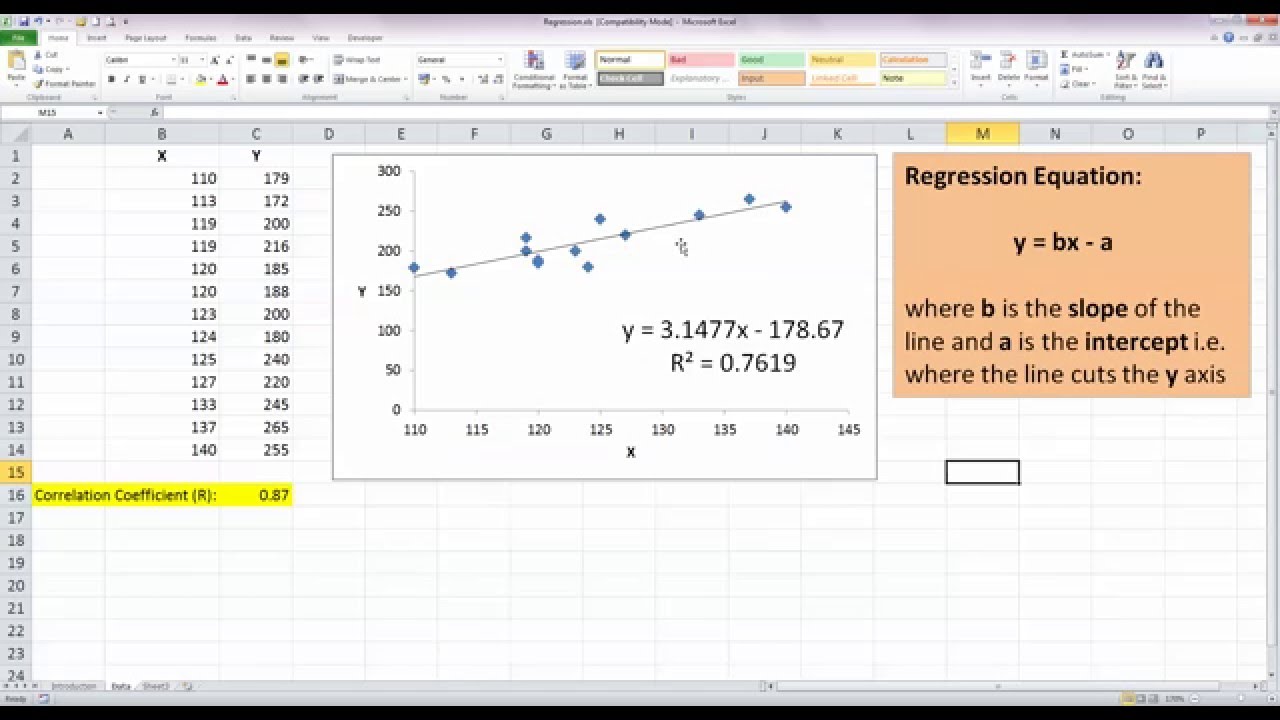
What we haven’t mentioned, so far, is that, in our model, there are coefficients. The more years you study, the higher the income you will receive. Let’s go back to the original linear regression example. Hence, it is unfit for regression analysis. Therefore, a causal relationship like this one is faulty, if not plain wrong. Moreover, high school and college take the same number of years, no matter your tax bracket. Putting high tuition fees aside, wealthier individuals don’t spend more years in school. This would mean the higher your income, the more years you spend educating yourself. Now, let’s pause for a second and think about the reverse relationship. You want to get a higher income, so you are increasing your education. This relationship is so trivial that it is probably the reason you are reading this tutorial, right now. The more education you get, the higher the income you are likely to receive. There is a causal relationship between the two. The dependent variable is income, while the independent variable is years of education. Think about the following equation: the income a person receives depends on the number of years of education that person has received. Whenever there is a change in X, such change must translate to a change in Y. When using regression analysis, we want to predict the value of Y, provided we have the value of X.īut to have a regression, Y must depend on X in some way.
Y is the variable we are trying to predict and is called the dependent variable. The easiest regression model is the simple linear regression: Y is a function of the X variables, and the regression model is a linear approximation of this function. There is a dependent variable, labeled Y, being predicted, and independent variables, labeled x1, x2, and so forth. Finally, you use the model you’ve developed to make a prediction for the whole population.Then, you can design a model that explains the data.The Process of Creating a Linear Regression Regression models are highly valuable, as they are one of the most common ways to make inferences and predictions. A linear regression is a linear approximation of a causal relationship between two or more variables. We will also develop a deep understanding of the fundamentals by going over some linear regression examples.Ī quick side note: You can learn more about the geometrical representation of the simple linear regression model in the linked tutorial.
#Find linear regresion for only one part of line in excel mac how to#
Along the way, we will learn how to build a regression, how to interpret it and how to compare different models.
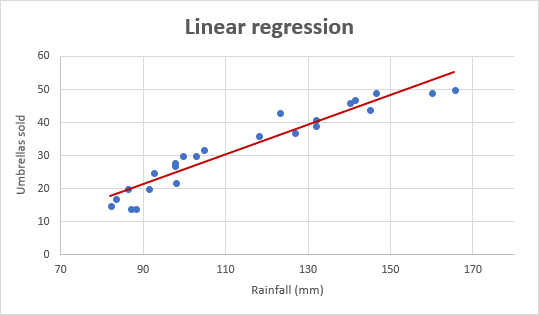
We’ll start with the simple linear regression model, and not long after, we’ll be dealing with the multiple regression model. We will use our typical step-by-step approach. You can quantify these relationships and many others using regression analysis. In the same way, the amount of time you spend reading our tutorials is affected by your motivation to learn additional statistical methods. “The amount of money you spend depends on the amount of money you earn.” Therefore, it is easy to see why regressions are a must for data science. Moreover, the fundamentals of regression analysis are used in machine learning.

And it becomes extremely powerful when combined with techniques like factor analysis. There are also many academic papers based on it. It is applied whenever we have a causal relationship between variables.Ī large portion of the predictive modeling that occurs in practice is carried out through regression analysis. Regression analysis is one of the most widely used methods for prediction.


 0 kommentar(er)
0 kommentar(er)
